Abstract
Recombination of Drosophila melanogaster is a fundamental biological process with profound evolutionary implications. Theory predicts that recombination increases the efficiency of selection in natural populations. However, direct tests of this prediction have been restricted to qualitative trends due to the lack of detailed characterization of recombination rate variation between genomes and within species. The use of imprecise recombination rates can also bias population genetic analyzes designed to assess the presence and mode of selection across genomes. Here we report the first high-resolution integrated description of genomic and population variation in recombination, which also distinguishes between the two outcomes of meiotic recombination: crossing over (CO) and gene conversion (GC).
We characterized the products of 5,860 female meioses in Drosophila melanogaster by genotyping a total of 139 million informative SNPs and mapping 106,964 recombination events at down to 2-kilobase resolution. This approach allowed us to generate genome-wide CO and GC maps, as well as a detailed description of the variation in recombination between individuals of this species. We describe many levels of variation in recombination rates. On a large scale (100 kb), CO rates exhibit extreme and highly punctuated variation along chromosomes, with hot and cold spots. We also show a wide intraspecific variation in CO landscapes that is associated with low-frequency hotspots in our sample.
GC rates are more evenly distributed across the genome than CO rates and are detectable in regions with reduced or absent CO. On a local scale, recombination events are associated with numerous sequence motifs and tend to occur within transcriptional regions, suggesting that chromatin accessibility favours double-strand breaks. All these non-independent layers of variation in recombination between genomes and between individuals must be taken into account to obtain relevant estimates of recombination rates and must be included in a new generation of population genetic models of the interaction between selection and linkage.
Method
Recombination rates are often estimated based on the relationship between the physical and genetic maps of the Drosophila genome. Early estimates of recombination, such as the adjusted exchange coefficient (Kindahl 1994) were based on cytological markers in combination with estimates of DNA content from the optical densities of polytene chromosomes (Sorsa 1988). Other techniques such as RTE (Hey and Kliman 2002) use transposable elements as markers on the physical map (Ising and Block 1984). However, with the availability of the complete genome sequence, the physical map of the genome is much more precise, facilitating a more precise estimate of recombination rates in D. melanogaster (Hey and Kliman 2002; Marais et al. 2001). ).
Recombination rates are now estimated by plotting Marey maps of the genetic positions of molecular markers (in centimorgans, cM) versus their physical position (in megabase pairs, Mbp). The recombination rate at any given nucleotide coordinate is estimated by taking the slope of the curve relating the genetic map to the physical map in one of two ways. A sliding window approach could be employed, in which a linear function is used to fit genetic position as a function of physical position within a window of a given size along a chromosome arm.
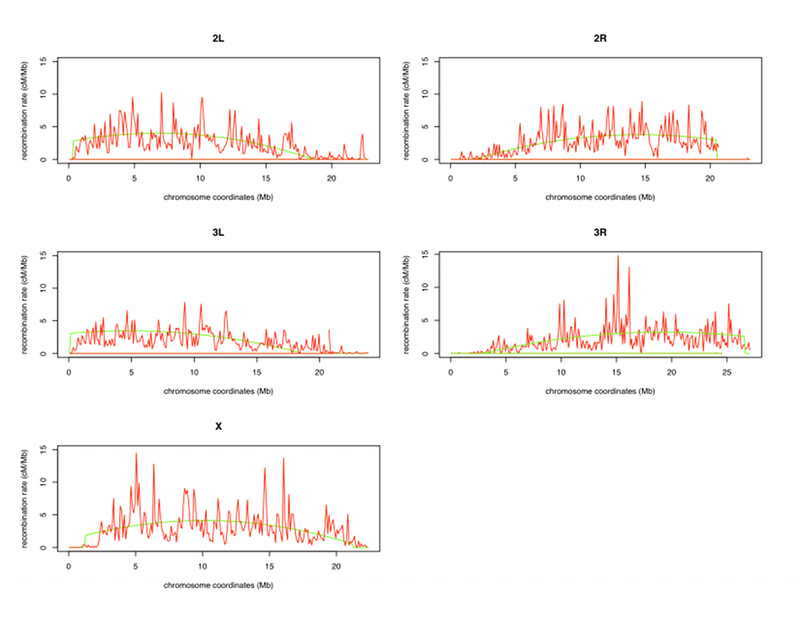
With this approach, the slope of this linear function within the window is taken as the local recombination rate. Alternatively, the genetic position of markers can be mapped as a function of physical position using a polynomial curve of degree n along an entire chromosome arm. Under this approach, recombination is estimated at a single nucleotide coordinate as the derivative of the polynomial curve of degree n. While the polynomial curve approach is less sensitive to regional variation in recombination rates than the sliding window approach, it is more resistant to errors in physical and genetic maps.
To correct for the calculated recombination rate for telomere and centromere regions that may be skewed, we start from each telomere and fit the data with the third-order polynomial with an increasing number of points from the telomere. The R-squared starts near 1, but at some points drops off precipitously. That is the point where we define the telomere/non-telomere transition. In most cases, recombination rate estimates for the telomeric region are close to zero, so we simply define the telomeric recombination rate as zero.
For centromeric regions, we define the transition to a zero recombination rate at the point at which the recombination rate estimate based on the third-degree polynomial becomes negative. We then recalculated the regression for each chromosome arm without defining the two limb regions. The R-squared differences for all points and using only the points outside the telomeric and centromeric regions are not substantial. To give you an example with chromosome 2R, the R-squared for all points is equal to 0.9929 and for points outside the telomeres and centromeres, it is 0.9916. This last step allows the recombination rates to be readjusted to the experimentally observed recombination rates in the telomere and centromere regions.
